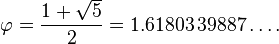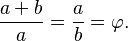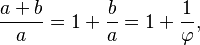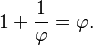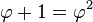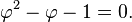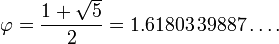Rasio Emas

12/11/2013 07:11

Rasio emas

Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Langsung ke: navigasi, cari
Ruas garis dalam rasio emas
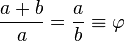Sebuah persegi panjang emas dengan sisi panjang a dan sisi pendek b, jika diletakkan berhimpitan dengan bujur sangkar dengan panjang sisi a, maka akan menghasilkan kemiripan persegi emas dengan sisi panjang a + b dan sisi pendek a. Hal ini dirumuskan melalui persamaan matematika \frac{a+b}{a} = \frac{a}{b} \equiv \varphi.
Cara menggambar sebuah persegi panjang emas:
1. Buatlah gambar sebuah bujur sangkar/persegi (merah).
2. Tarik satu garis memotong tepat di tengah persegi membaginya menjadi 2 bagian.
3. Tarik garis dari titik perpotongan garis tengah dengan sisi persegi ke sudut persegi (panah abu-abu), jadikan ini sebagai jari-jari lingkaran.
4. Dengan menggunakan jangka buatlah satu lingkaran dengan pusat di titik perpotongan sesuai jari-jari, lingkaran menyentuh dua sudut persegi.
5. Tarik satu garis baru sesuai sisi persegi hingga berpotongan dengan lingkaran, buat persegi panjang baru berdasarkan titik pertemuan sisi-sisi ini (biru). Gabungan persegi dengan persegi panjang membentuk persegi panjang emas.

Dalam matematika dan seni, dua nilai dianggap berada dalam hubungan rasio emas (\varphi) jika rasio antara jumlah kedua nilai itu terhadap nilai yang besar sama dengan rasio antara nilai besar terhadap nilai kecil. Nilai yang lebih besar dilambangkan dengan huruf a, sedangkan nilai yang lebih kecil dilambangkan dengan huruf b. Gambar di sebelah kanan menggambarkan hubungan geometrik yang jika dirumuskan secara aljabar adalah sebagai berikut:

\frac{a+b}{a} = \frac{a}{b} \equiv \varphi,

dimana huruf Yunani phi (\varphi) mewakili rasio emas. Nilainya adalah:

\varphi = \frac{1+\sqrt{5}}{2} = 1.61803\,39887\ldots.

[1]

Setidaknya sejak Abad Renaisans, banyak seniman dan arsitek telah membuat proporsi karya sesuai dengan rasio emas—terutama dalam bentuk persegi emas, yaitu perbandingan sisi panjang terhadap sisi pendek sesuai dengan nilai rasio emas—dipercaya proporsi ini secara estetika sangat ideal. Sebuah persegi panjang emas dapat dipotong menjadi persegi dan persegi panjang kecil dengan rasio aspek yang sama persis. Para ahli matematika sejak zaman Euclid telah mempelajari rasio emas karena sifatnya yang unik dan menarik. Rasio emas juga digunakan dalam analisis pasar keuangan, serta strategi seperti retraksi Fibonacci.

Rasio emas sering kali disebut bagian emas (Latin: sectio aurea) atau rata-rata emas.[2][3][4] Nama lainnya antara lain rasio ekstrem dan rata-rata,[5] bagian tengah, proporsi ilahiah, bagian ilahiah (Latin: sectio divina), proporsi emas, potongan emas,[6] angka emas, dan rata-rata Phidias.[7][8][9]

Perhitungan

Templat:Bilangan irasional
Biner 1.1001111000110111011...
Desimal 1.6180339887498948482...
Heksadesimal 1.9E3779B97F4A7C15F39...
Pembagian berkelanjutan 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}}
Bentuk aljabar 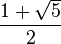\frac{1 + \sqrt{5}}{2}
Seri infinit 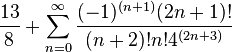\frac{13}{8}+\sum_{n=0}^{\infty}\frac{(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}

Dua nilai a dan b dinyatakan berada dalam hubungan rasio emas φ jika:

\frac{a+b}{a} = \frac{a}{b} = \varphi.

Salah satu cara untuk menemukan nilai φ adalah dengan memulai pembagian sisa. Dengan cara menyederhanakan pembilang dan penyebutnya dalam b/a = 1/φ,

\frac{a+b}{a} = 1 + \frac{b}{a} = 1 + \frac{1}{\varphi},

hal ini menunjukkan

1 + \frac{1}{\varphi} = \varphi.

Dikalikan dengan φ menghasilkan

\varphi + 1 = \varphi^2

yang dapat diatur menjadi

{\varphi}^2 - \varphi - 1 = 0.

Dengan menggunakan formula kuadrat menghasilkan jawaban positif yaitu

\varphi = \frac{1 + \sqrt{5}}{2} = 1.61803\,39887\dots.
Back